SHORT ANSWER: from preschool level right up to super-expert level, maths can be broken down into three main branches: number, shape and patterns. Algebra is simply the language of patterns.
LONG ANSWER: Now let’s take an example: which of these two rectangles has the larger AREA (which is a fancy mathsey way of asking which ones takes up more space on the page)? I’ve drawn the rectangles on centimetre-squared paper, so to see which is biggest we can just count the squares. A quick count reveals that the one on the left contains 21 cm2 whereas the one on the right contains 20 cm2, so the rectangle on the left is larger!
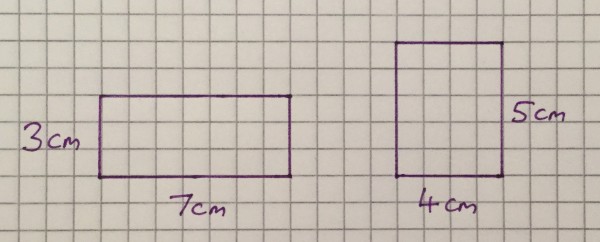
At this point, your maths teacher might decide to give you pages and pages of rectangles and ask you to work out their areas – after all, figuring out how big rectangles are is a very useful skill for:
But if you know your times tables then pretty quickly you would spot a pattern: you don’t need to count the squares, you just count how long and how tall each rectangle is, and then MULTIPLY THESE TWO NUMBERS TOGETHER! When you spot this pattern, you have done something much cleverer than mere arithmetic: you have figured out how something works, which is really the point of advanced maths. You will probably want to write this pattern down so that you can show it off to your friends. You could write something like this:
To figure out how big a rectangle is, just multiply the length by the width.
That’s quite a lot of writing for such a simple pattern! How about shortening it a little:
Area of rectangle = length x width.
But now let’s make it even better still: we’ll just write “A” instead of “Area” – everyone will know what we mean. Similarly we can use “l” and “w” for “length” and “width”:
A = l x w
Awesome! We can even skip the times sign: in maths, if two letters are put next to each other then that means “multiply” anyway:
A=lw
Boom! We have just used algebra: the language of patterns!! Here are four more of my favourite patterns, and they all use letters to stand for whole words, which makes them much much easier to write down:
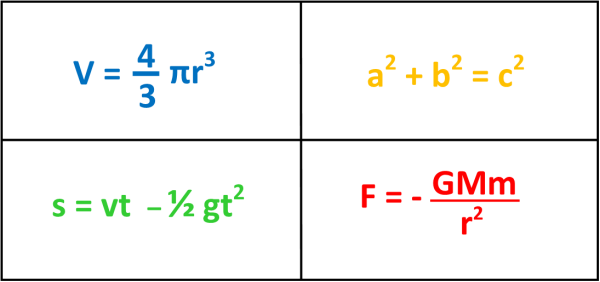
BLUE: this is the formula for the volume of a sphere. It can tell you how much snow you need to make a giant snowball.
GOLD: this is Pythagoras’ Theorem, a pattern about how long the sides of right-angled triangles are. It can tell you how far you need to walk between two points on a map.
GREEN: if you time how long a juggling ball spends in the air, this pattern can tell you how high you have just thrown it.
RED: this is Newton’s law of gravitation. Newton is one of my Superstars of Maths – more about Newton here.
Maths and science are all about finding patterns to figure out how the world works, and algebra is the language of patterns. Here’s how to organise a school visit so you can find out more.
Comments welcome, please visit the House Of Maths Facebook Page
[mc4wp_form id=”399″]