House of Maths School Workshops Primary & Secondary in Dorset & South - SUPERSTARS OF MATHS – RENE DESCARTES

This handsome chap is Frenchman Rene Descartes (1596-1650), who famously said “I think therefore I am”.

If you’re thinking about what he might mean by this, then it apparently means you exist – great news and congratulations!!

But the reason Descartes is my “hero of maths” for this month is because he also gives his name to CARTESIAN GEOMETRY – which is what you do when you plot the point (4,3) on a graph by going “along the corridor and up the stairs”. By the way, “Geometry” is a posh word for “Shapes”.

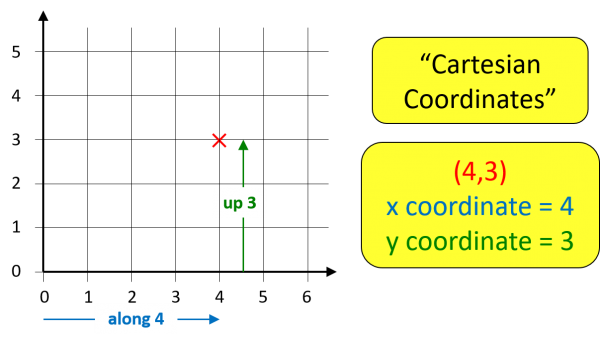
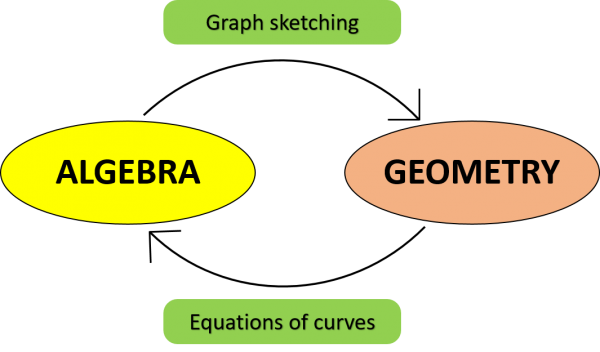
Now, Descartes’ new Geometry goes much further than just changing pairs of numbers to points on a graph: his big discovery was a way to switch between Shapes and Algebra – giving you a two-pronged way to attack any problem in either algebra or shape.

If you have a nasty great big algebraic expression with lots of x’s in it, like y = 3x² + e^x – sin(x) then Descartes’ invention allows you to represent it on a graph, turning it into a shape. And conversely, if you have a straight line, a circle, or any sort of crazy curve such as the path you follow on the Sizzler ride at the fairground, then Cartesian Geometry allows you to turn it into an algebraic equation. This allows you to use the full power of algebra on your curve, giving you a much larger toolbox of mathematical techniques to analyse your curve.

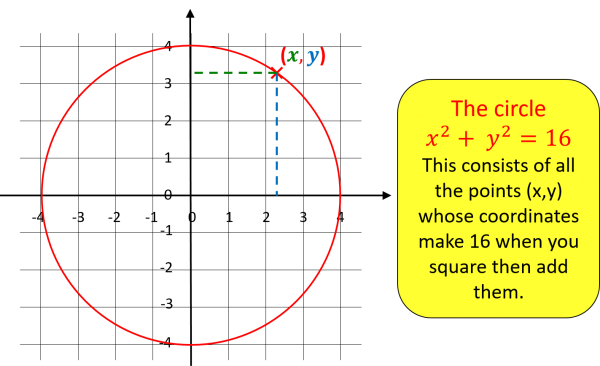
When we first learn to count, numbers can seem a bit abstract, but we quickly learn how to think of numbers as points on a “number line” – giving us a way to “picture” adding and taking away as moving forward or backwards along the number line. In the same way, Descartes’ work gives us a clever way to picture algebra! Here’s an example from the start of A-level maths, where a circle becomes an algebraic equation.

By the way, it was also Descartes’ idea to use little numbers, or “indices”, to represent repeated multiplication, so when 7³ = 7 x 7 x 7 the little 3 – pronounced “cubed” – is Descartes’ idea.

If you’ve enjoyed this blog, why not invite House Of Maths into your Primary or Middle school for a whole day of Maths Shows, Workshops and Assemblies? Thanks for reading and see you next month!

NOTIFY ME OF NEW POSTS BY EMAIL (approx. one a month):

[mc4wp_form id=”399″]