House of Maths School Workshops Primary & Secondary in Dorset & South - 6 WAYS TO MAKE MATHS FUN

HOW CAN I MAKE MATHS FUN?

House Of Maths was recently interviewed on the radio about the new GCSE and “real life” maths problems. But while making maths relevant IS important, “keeping it real” doesn’t automatically make maths fun – especially if your teacher is more like Miss Trunchbull than Miss Honey. Instead, here are the six ACTUAL secrets of turning maths from boring to brilliant:

1. SMILE & BE PASSIONATE! Do this when you talk about maths, and everyone else will enjoy themselves more too – yes that’s right, smiling really is infectious! Brian Cox, Johnny Ball, Rachel Riley and Drs Chris & Xander van Tulleken are all experts at talking passionately about their subject. Be sure to catch the R.I. Christmas Lectures on TV each year if you want to see some great science and maths communicators in action!

Now you’re starting to have fun, the next two tips will help to make maths less abstract:

2. MAKE MATHS A MULTI-SENSORY EXPERIENCE: when people understand a new idea, they often say “I see” or “I get it”. So instead of maths being something which only happens inside your head, make sure students can see maths with their eyes, or even feel in their hands. Drawing pictures is essential in maths – from learning to count on a NUMBER LINE right up to A-level and beyond, where GRAPH SKETCHING gives us a way to literally picture algebra. And to really feel your way around the subject you’ll also need to…

3. USE FUN PROPS: some of my favourite props to use are:

• DICE: great for counting, adding, multiplying and probability (Primary), probability (GCSE) and Normal Distributions (A-level). Try rolling one, two or three at a time, add the scores and keep a tally chart of what happens.
• POLYDRON: colourful plastic triangles, squares, pentagons and hexagons. Here’s the Poydron website. Use them to learn about corners, sides, colours & symmetry (Primary), tessellations (KS3), then clip them together to learn about faces, edges, vertices (GCSE) and Euler’s Theorem (A-level)
• 3D SHAPES: when discussing properties of 3D shapes, it certainly pays to have actual hemispheres, pyramids & cubes that you can pick up and touch close to hand.
• PEOPLE: that’s right, use of volunteers in a maths demonstration can reassure your audience that you’re not cheating, provide an extra pair of hands, and be really funny: especially if they have to wear something funny or do something “dangerous”.

Some of my other favourite props to use in maths demos include balloons, juggling balls, pulleys, funny hats and even buckets of water.

4. TURN PROBLEMS INTO PUZZLES: a mathematician isn’t someone who finds maths easy, it’s someone who enjoys that it’s hard. But luckily for maths, humans have evolved to enjoy solving puzzles, so one way to make maths fun is to turn problems into puzzles.

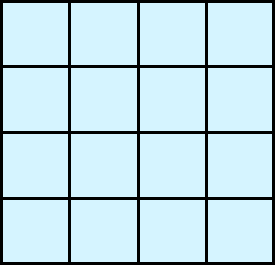
Try this puzzle, for instance: all you need to do is count how many squares there are in this picture (answer at the end if you need it, but do have a go first – no cheating!).

This sort of simple puzzle is hugely popular on Social Media like Instagram and Facebook, despite being a maths workout. A-level students might like to find how many squares in total in a 10×10 grid? For Further Maths A-level: how about n by n?

5. TELL STORIES: maths has been blessed with some amazing personalities, and sharing their stories can really help to bring maths to life. Can you match these five great mathematicians with their stories?:

6. BOOK A HOUSE OF MATHS VISIT FOR YOUR SCHOOL: if this all sounds like hard work, it is! – but House Of Maths is here to help! A typical School Visit will include maths shows and / or maths workshops, so why not enquire about a booking today?  – I look forward to seeing you all soon!

CONCLUSION: maths can seem abstract, so as teachers we must use passion, pictures, props, playful puzzles and even stories to bring it to life. I hope this article will give you some ideas of how to do that.

Answer to “how many squares” puzzle: the 4×4 grid has 16 little squares, nine 2×2’s, four 3×3’s and one big 4×4 square (the whole shape), so 4² + 3² + 2²  + 1² = 30 squares in total. The pattern in general for the nxn grid: the formula for the sum of the first n squares is 1/6 n(n+1)(2n+1) squares in total.

NOTIFY ME OF NEW POSTS BY EMAIL (approx monthly):

[mc4wp_form id=”399″]