INTRODUCTION: imagine a tightrope walker: she can only change her position in one direction: forwards & backwards, so we need just one number – how far along the rope she is – to specify her position. That’s one dimension!
Now picture an ant crawling on a tabletop: the ant can crawl forwards & backwards or left & right, and we now need two numbers (e.g. the ant’s horizontal and vertical distance from a particular corner of the table) to pinpoint exactly where the ant is. That’s an extra degree of freedom: two dimensions!
And finally, picture yourself wearing a jetpack: you can now move freely in all three of our spatial dimensions: forwards & back, left & right, AND up & down. Three numbers are now required to describe your position at a given time e.g. latitude, longitude and altitude. That’s three dimensions!
If you think that sounds fun, imagine how cool it would be if there was a fourth, new direction in which you could also travel! What would 4-dimensional space look like, and what sort of shapes would inhabit it?
TESSERACT: the next word in the sequence: square, cube, …? The edge of a square consists of four line-segments; the surface of a cube consists of six squares; so the “hypersurface” of a tesseract consists of eight cubes!
If $x^2$ is called $x$ squared, and $x^3$= is called $x$ cubed, then maybe $x^4$ should be called “$x$ tesseracted”?!
Here are some attempts by us mere humans to draw a tesseract, based on the idea that you can draw a cube by connecting corresponding corners of two slightly offset squares; these tesseracts are made by connecting corresponding vertices of two slightly offset cubes.

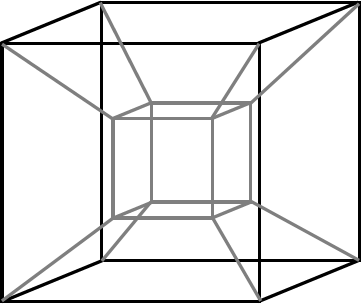
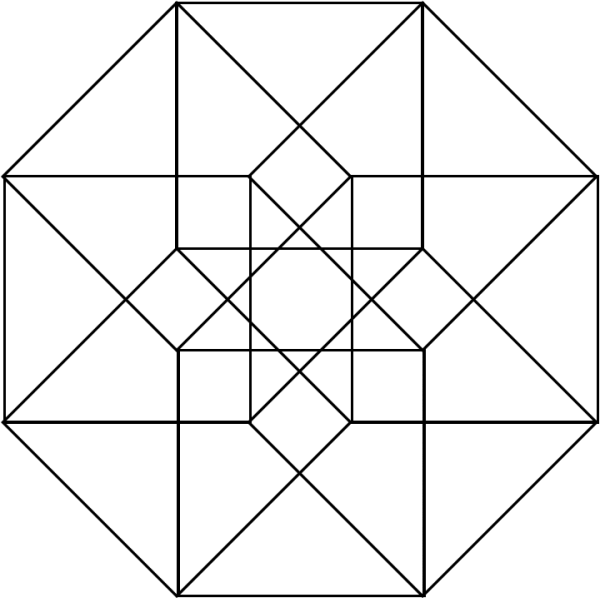
DALI CROSS: a “net” of a tesseract, consisting of 8 cubes which we imagine might “fold up” to make a tesseract in the same way that the cube net shows consists of 6 squares which fold up to make a cube. Named after the artist Salvador Dali, who used one in his 1954 surrealist painting “Corpus Hypercubus”. There are 11 different nets of a cube, and 261 distinct octocubal nets of a tesseract. So there! Thank you Stella Software and Wikimedia.org for this fab image of the Dali Cross!

cube net 1

cube net 2
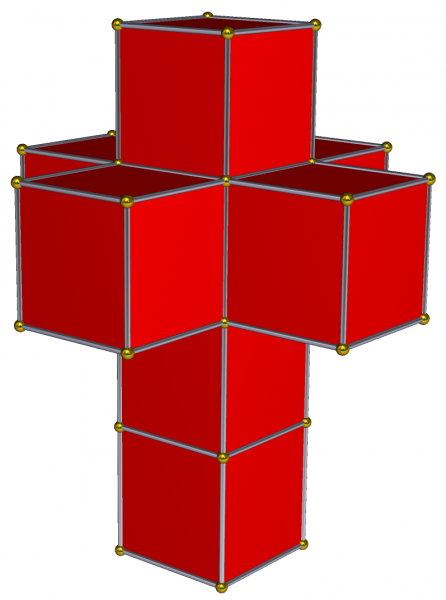
DALI CROSS
HYPERCUBE: the n-dimensional analogue of the word “square”. Squares, cubes and tesseracts are all types of hypercube.
POLYTOPE: the generalisation of a polyhedron (“many flat sides / faces”) to 4 or more dimensions. A polygon (e.g. triangle, octagon) is a 2D object whose boundaries are line-segments, a polyhedron (e.g. cube, pyramid) is a 3D object bounded by polygons, and so a POLYTOPE, (e.g. tesseract, see later for another example) for any being lucky enough to inhabit four spatial dimensions, would be a 4D object whose boundaries are polyhedra.
CELL: the next word in the sequence vertex, edge, face, …? The two boundary points of an edge are called vertices; the three or more boundaries of a face are called edges, the four or more boundaries of a polyhedron are called faces, and the five or more boundaries of a 4D polytope are called “cells“. A tesseract is bounded by 8 cube-shaped cells, in the same way that a cube is bounded by 6 square-shaped faces.
HYPERPLANE: scatter graphs in 2-dimensional space have a line of best fit; in 3-D space our points on a scatter graph could have a plane of best fit; andin 4D space we’d have to fit a … what’s the word?… oh yes, a “hyperplane” of best fit!
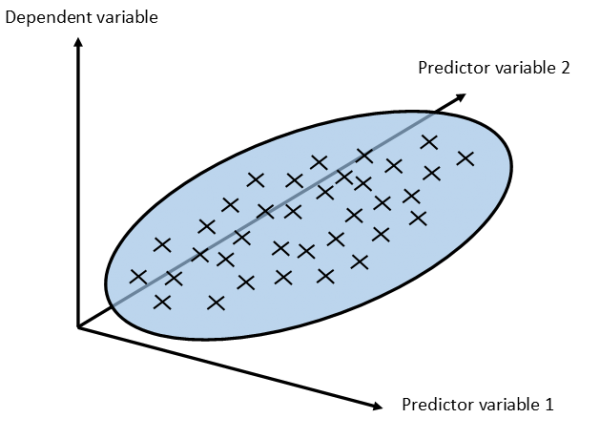
A plane of best fit on a scatter graph with two predictor variables. But what would a hyperplane-of-best-fit look like on a scatter graph with three or more predictor variables?
SIMPLEX: the next word in the sequence line segment, triangle, tetrahedron,…? A triangle is a polygon bounded by three line segments; a tetrahedron is a polyhedron bounded by four triangles; and so a 4-Simplex is a “polytope” (see above!) bounded by five tetrahedra. The 5D version is called a 5-Simplex. I’ve often taught the “Simplex Algorithm” to my A-level students, but never really “got it” until reading an explanation of how the algorithm works in relation to a multi-dimensional polytope. Now I can more or less visualise it in geometric terms, and it kinda makes sense.
WHAT’S THE POINT?: mathematics often appears to be the study of numbers, but numbers merely allow us to study pattern and structure – the real aim of maths. This often leads to powerful but abstract concepts, best described by algebra but easiest to “see” using a different branch of mathematical study: Geometry – the study of shape! Using geometrical visualisations to describe algebraic concepts is such a powerful tool that it would be a crime to limit its study to just the three spatial dimensions that we happen to live in. Hence all of the marvellous mathematical inventions in this glossary. Read more about linking algebra and geometry here.