 For anyone unfamiliar with the song:
For anyone unfamiliar with the song:
“On the first day of Christmas my true love gave to me: a Partridge in a Pear Tree”: 1 gift.
“On the second day of Christmas my true love gave to me: Two Turtle Doves and a Partridge in a Pear Tree”: this is another 2+1=3 gifts, so 4 gifts in total so far.
On the third day I’m given Three French Hens, a further two Turtle Doves, and another Partidge in a Pear Tree; so 3+2+1=6 gifts on day three, making 1+3+6=10 gifts in total so far. The song continues all the way to “12 Drummers Drumming” on day 12.
The keys to working out the total number of gifts over all 12 days are the Tetrahedral numbers, which are made up from the Triangular numbers.
Here are the first few Triangular numbers. The ‘nth’ triangle number is simply the number of balls required to make a triangle with ‘n’ rows:
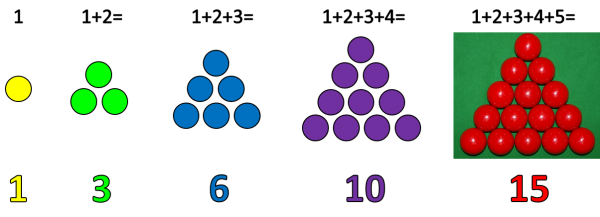
And these are also the number of gifts that my true love gave to me on each of the first five days of Christmas! For instance, on the fifth day I was given 5 (gold rings) + 4 (calling birds) + 3 (French hens) + 2 (turtle doves) + 1 (partridge in a pear tree) = 15 gifts.
Now, to find out the total number of gifts for all twelve days, we need to add up the first twelve of these Triangle numbers: so 1+3+6+10+15+… all the way up to the twelfth term. Adding up the first ‘n’ triangle numbers gives you the ‘nth’ TETRAHEDRAL NUMBER. Here are the first few Tetrahedral numbers. The ‘nth’ tetrahedral number is simply the number of balls (or Clementines) required to make a TETRAHEDRON (Triangle-based Pyramid) with ‘n’ rows:

And these are also the number of gifts that my true love gave to me up to and including each of the first three days of Christmas! For instance, by the third day I’d received 1 (on the first day) + 3 (on the second day) + 6 (on the third day) = a total of 10 gifts up to and including the third day.
To solve our puzzle, we need the total number of gifts up to and including the twelfth day (the last day in the song), so we need the twelfth Tetrahedral number. Using a little algebra from A-level maths, it’s possible to work out a formula for the ‘nth’ tetrahedral number, allowing us to jump straight to the one we need without working out all the others in between:
T(n) = (1/6)(n)(n+1)(n+2)
Replacing ‘n’ with the number 12 in this formula (we call this ‘substitution’), the twelfth tetrahedral number – and the answer to our puzzle – is T(12) = (1/6)(12)(13)(14) = 364, or one gift for every day of the year except for Christmas Day itself!

Out of interest, here is a tower of Ferrero Rocher chocolates I snapped in the local supermarket.
There was one chocolate on the first row, then 3 on the next, then 6, then 10 etc. Assuming the tower is solidly filled with the chocolates, the total number of chocolates in this tower is T(17), the 17th tetrahedral number, which works out to be 969 chocolates – just what you need if you have lots of family visiting over the Festive Period.
Now I just have to figure out what to do with all those Partidges in all those Pear Trees. Merry Christmas to all!
Comments welcome, please visit the House Of Maths Facebook Page
[mc4wp_form id=”399″]