NUMBERS: are an abstract idea used to measure e.g. how many? How big? Or numbers can point to a position on a number line. Here are some examples of numbers: $4, \frac{3}{8}, 0.157, \pi, -\sqrt{2}, $ fifty-nine. There are infinitely many different numbers.
NUMERALS: are the words or symbols that we use the represent our numbers. The list above is really a list of numerals. I could represent the number 4 using a numeral or by clapping my hands four times, or by holding up four fingers.
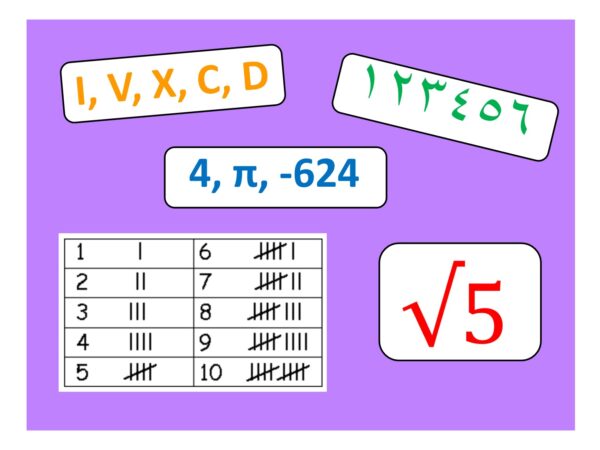
DIGITS: are the ten single symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 that we use to represent numbers. You cannot split them apart into separate symbols. For instance: two hundred and seven (or 207) is one numeral that needs the three digits 2, 0, 7 to write it, and represents the idea of a particular number. These ten digits are used almost everywhere in the modern world, and originate from India in the 6th or 7th century (a long time ago!). If you want to be all fancy about it, they are the Hindu-Arabic Numerals.
A FUN RIDDLE TO TRY ON THE SCHOOL SMARTY-PANTS: can you list all the digits of pi? Pi (pronounced “pie” and usually written using the Greek letter π) famously goes on forever when you try to write it as a decimal. Here are the first 50 digits of the decimal version of pi: 3.14159265358979323846264338327950288419716939937510…
Trying to write it out “in full” is impossible (this amazing result is proved in the A-level maths course!). But we can easily answer the riddle: Yes, I can list all the digits of pi: they are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Of course they all appear multiple times, but they are all the digits!
ARE THERE OTHER DIGITS? Yes! Your fingers and thumbs are also sometimes called your “digits”. You (probably) have ten of those, like the ten numerical digits.
YET MORE NUMERALS AND DIGITS: in much of the Middle East, clocks and car number plates use these ten digits (or Eastern Arabic Numerals):
TALLIES: You have probably also met tallies before: these look like matchsticks placed in a row and are used to keep count when you’re in a hurry. You use the fifth line to “close the gate” : see the box in the image. Tallies are of course numerals that represent numbers, but how many of them are single, individual digits? It would be reasonable to argue that only the first one is: all the others are many ones placed together. But I would argue that there are two different digits in play here: namely the symbols for 1 and 5. All other tallies are combinations of those two digits.
WHAT ABOUT ROMAN NUMERALS? The ancient Romans didn’t use our modern digits – or the Eastern Arabic ones. Instead they had six basic “numerals” which would combine to make other “numerals”. The seven fundamental Roman Numerals are: I, V, X, L, C, D, M (equivalent to our modern 1, 5, 10, 50, 100, 500, 1000). Larger numbers like 13, 26 and 2022 can also be represented using Roman Numerals, like this: XIII, XXVI, MMXXII. These combinations are also “numerals”, because a numeral is any symbol, figure or group of symbols used to represent a number. Roman Numerals are completely useless for doing any sensible maths (there are zero famous Ancient Roman Mathematicians!) but Roman Numerals have survived mainly because they are so weird and can make you look sophisticated. Also people like the way they look on clocks.
SOME PUZZLES: