House of Maths School Workshops Primary & Secondary in Dorset & South - THE TEN COMMANDMENTS OF MATHS

Isn’t maths great? Everything is either right or wrong, it all makes sense and as long as you follow the rules everything will be ok. Right? Umm… no.

Here are my Ten Commandments of Maths: all were considered to be obviously correct at one time but, as we shall see, rules are made to be broken.

1) Zero is the smallest number; there shall be no numbers smaller than it.

2) Infinity shall be the largest number; there shall be no number larger than it.

3) Thou shalt not divide by zero.

4) All numbers may be written as fractions.

5) Parallel lines never meet, no matter how far they shall be extended.

6) The sum of the angles in a triangle shall always be 180 degrees.

7) All things in maths shall be either right or wrong.

8) Thou shalt not square root negative numbers (I explain what this means later on!).

9) Thou shalt take the factorial of only whole numbers (ditto!).

10) Though shalt always read the question.

Maths has a long history of obvious statements turning out to be false, often leading to new branches of maths. So here’s a 21^st Century take on my Ten Commandments:

1)         Negative numbers were gradually introduced over a period of many centuries, but mathematicians were slow to accept them, describing them variously as “false”, “meaningless”, and “inappropriate – people do not approve”. But they’re great for describing debts, heights below ground level and really cold temperatures, and for helping me to do my sums. Today even Primary School children will happily embrace numbers “smaller than zero” despite the fact that they clearly don’t exist (unless you can show me “minus two sheep”?).

2)         For a start, infinity is not a number: if it was then infinity plus one would also equal infinity; subtracting infinity from both sides we then get a problem: zero=one. To compound the problem, Georg Cantor showed in 1891 that there is more than one flavour of infinity: that’s right, some infinities are “larger” than others.

3)         What is 3 divided by zero? In other words, what do we have to multiply zero by to get three? This is of course impossible – whatever we multiply zero by we will only ever get zero, never 3 – ask your calculator to try if you don’t believe me. But mathematicians did give meaning to the bizarre sounding sum “zero / zero” with the invention of calculus in the 17^th century, by considering it to be the limit of a sequence of sums which do have answers. It turns out that zero / zero can take any value you like, depending on how you approach the zeroes.

4)         This again turns out to be false – as the poor Greek mathematician Hippasus discovered in the fifth century BC. Unfortunately, Hippasus’ shipmates were so horrified at his discovery of “irrational numbers” that they threw him overboard and he was drowned at sea.

5)         Wrong again! It’s true if the lines are drawn on a flat surface (“Euclidian space”) but how about if we draw the lines on a sphere? In this case, the curvature of the sphere’s surface means the parallel lines will bend together, and ultimately meet. Einstein then discovered that even our 3-dimensional space is “curved”, laying the groundwork for his theory of gravity.

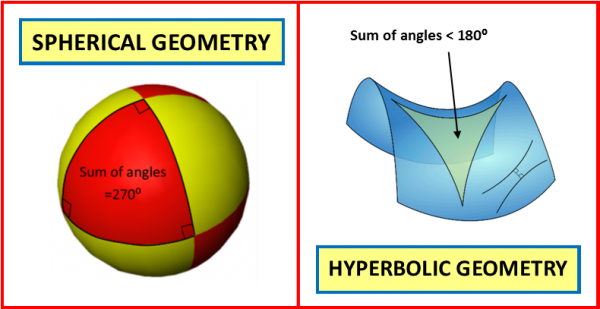
6)         TRUE: but only if drawn on a flat surface (“Euclidian Geometry”). But take a look at the red triangle drawn on this juggling ball (“Spherical Geometry”): each of the three angles is a right angle, so the angle sum is 270 deg! If you like eating crisps you can also try drawing triangles on a pringle (“Hyperbolic Geometry”), and in this case the angles will sum to less than 180 deg.

7)         To the utter horror of mathematicians, this too turned out to be problematic: Kurt Godel showed in the 1900’s that some mathematical theorems are undecidable: although a statement might be either right or wrong, sometimes it’s impossible for us to decide which! Try this one: “This statement is false”. Now, if the statement is true then it must be false, but if it’s false then it’s not false so it must be true!!! Statements like this have shaken the very logical foundations upon which maths is built, and have important consequences in philosophy and computing.

8)       To “square” a number you multiply it by itself, and the reverse of this process is the “square root”: so 5²=25, and the square root of 25 is 5. But what’s the square root of negative 25? Squaring both positive and negative numbers gives a positive answer:
5²=25
(-5)²=25

So what number can I multiply by itself to get negative 25?

Maths gradually came up with a solution by extending our number system again, this time to include “Complex Numbers”, which can be found not on the “real” number line, but floating above or below it, and in the 17^th Century, Leonard Euler came up with the symbol i that we still use today to denote the square root of minus one.

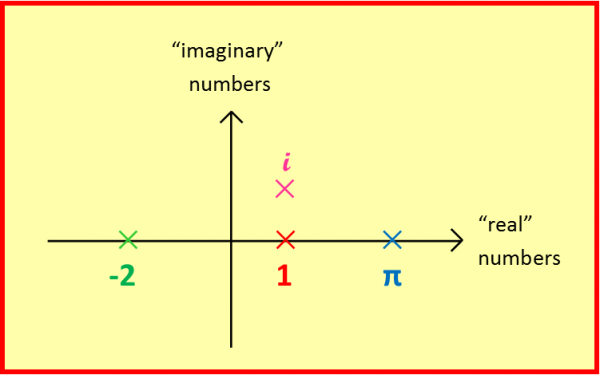
Complex numbers provide useful shortcuts for solving certain differential equations, and are commonly used to describe the flow of electricity, but are still referred to as “imaginary” today, acknowledging that, like negative numbers, they don’t really exist!

9)         It’s time to make really big numbers on your calculator, using the FACTORIAL button – so cool that the symbol for it is !

To get the factorial of a number, you simply multiply together 1 x 2 x 3 x … all the way up to your number. So 5! = 1x2x3x4x5.

But how would you find the factorial of 3.5, or of one-and-a-quarter? Again, maths found a way round this by inventing the “Gamma Function” (thanks again to Euler).

10)         At last: this one’s true! So yes, even in today’s world please do ALWAYS READ THE QUESTION!

CONCLUSION: I’ll leave the final words to two mathematical greats:

“God made the integers, all else is the work of man.”

(LEOPOLD KRONECKER 1823-91)

“The most dangerous phrase in the language is, ‘We’ve always done it this way.’”

(GRACE HOPPER 1906-1992).

NOTIFY ME OF NEW POSTS BY EMAIL (approx monthly):

[mc4wp_form id=”399″]