ER… Shall I run you past that again??
To illustrate what this means, let’s first try just putting the numbers down in numerical order:
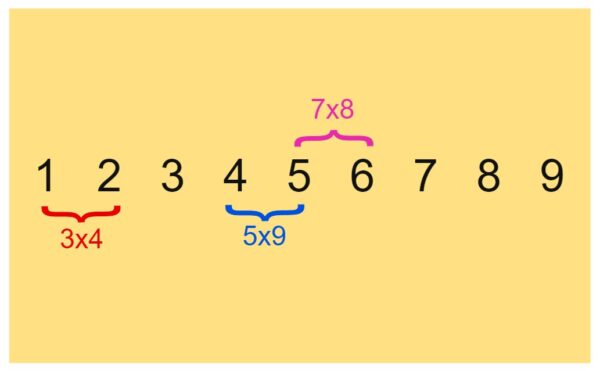
As you can see, three of the adjacent pairs appear as answers in the first ten times tables:
12=3×4 (or 4×3)
45=5×9 (or 9×5)
56=7×8 (or 8×7)
but most of the adjacent pairs do not e.g. the second pair is 23. This is NOT an answer in the first 10 times tables (in fact 23 is a prime number).
Note that in this puzzle, we are only going as far as 10×10. So you could not place the 9 next to the 6 to make 96=12×8, nor the 6 next to the 9 to make 69=3×23: neither of these are allowed.
I will give you two starting hints, which together make this a really good times table puzzle:
a) it can be done! …
b) … but only in one way!
That’s it, enjoy!
In case you get stuck, some hints follow. Scroll down if you like.
<
<
<
<
<
<
<
<
<
HINT 1: let’s look at the number 9. What can we pair it with? None of 91, 92, 93, …, 99 appear in the first 10 times tables, therefore nothing can follow the 9. This means that the 9 must go right at the end of the row.
One further hint follows:
<
<
<
<
<
<
<
<
<
HINT 2: what numbers could go next to the 7? In front you can only have 2, to make 27 (=3×9. None of 17, 37, 47, … are in the times tables). And following the 7 you can only have 2, to make 72 (=8×9. None of 71, 73, 74, … are in the times tables). 7 cannot go in the middle of the row because you can only use the 2 once – it can’t go before and after the 7. Therefore 7 must go at one end of the row. Since we already know 9 goes at the end, the 7 must therefore go at the start of the row. We now have:
Can you work it out from there? Good luck!