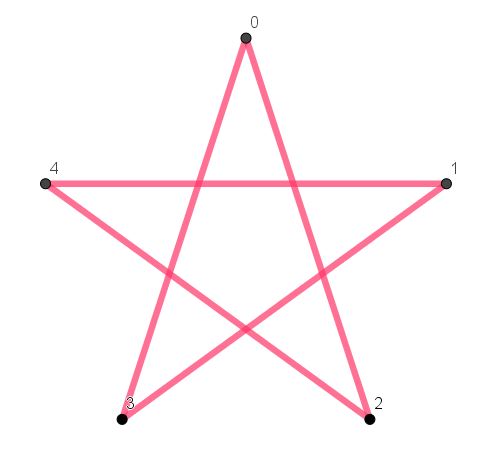
Star polygons are beautiful mathematical objects, a juxtaposition of maths and art. They’re also really easy to make: as an example here is a {5,2} Star Polygon. The first number tells us to start with 5 points (“vertices” or in the singular “vertex“) in a circle. It’s convenient to number them 0, 1, 2, 3, 4. (You can label them 1, 2, 3, 4, 5 if you prefer). The second number tells us which points to connect: you count on 2 places each time. So start at 0, join to 2, then 4, then 1, 3 and finally back to 0: the star is complete! Note that arithmetic behaves quite unusually when creating a star polygon: for example 4+2=1. Mathematicians call this modular arithmetic and it crops up all over the place, most obviously on clocks (e.g. 10 o’clock + 5 hours = 3 o’clock!!).
Have a look at the next three examples, then print off this star polygon worksheet so you can have a go making your own.
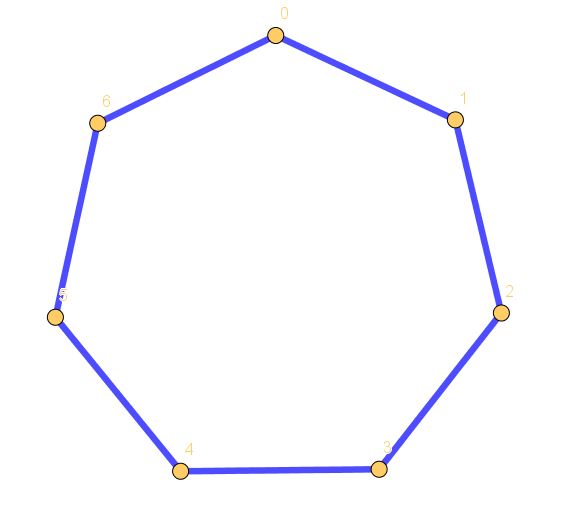
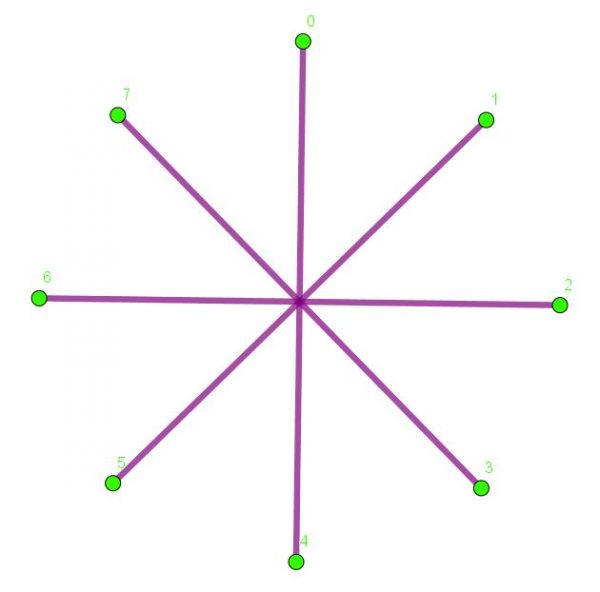
First we have a {7,1} star polygon. It’s just a regular heptagon, because you count on just one vertex each time. Next is an {8,4} star polygon: here we get back to zero after only two steps, so the star is simply made from four straight line segments.
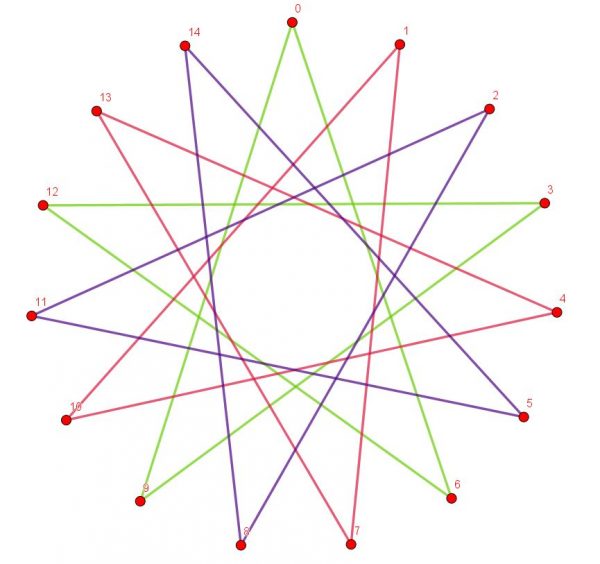
The final one is a {15,6} star polygon. Because 15 and 6 have a highest common factor (also called “greatest common divisor“) of 3, the start polygon will be in three pieces. I’ve emphasised this by drawing the three pieces in different colours, although using the same colour for all three pieces probably looks nicer!
BRAINBOXES ONLY: If the HCF of n and k is 1, then n and k are said to be coprime and the {n,k} star polygon will be in one piece. If you can figure out why this is then give yourself a mighty at on the back: you are well on your way to understanding modular arithmetic!
Print off this Star Polygon Worksheet, or better still have a play with Geogebra: the free software I used to create all the star polygons in the blog.
You can generalise this idea to making Star Polyhedra: here’s an example.

Finally, here are three National Flags that feature Star Polygons. Can you name both the countries, and the Star Polygons in {n,k} form? One of them is a hexagram – see also Hexahedra and other hex words for a discussion of Hexagrams.


