A Pythagorean Triple is a set of three positive integers (whole numbers) that satisfy Pythagoras’ Theorem $a^2+b^2=c^2$, such as {3, 4, 5} or {5, 12, 13} or {28, 45, 53}. It’s easy to see that there are infinitely many such triples: one way is to take multiples of the well-known {3, 4, 5} triple; multiplying each number by 2 or 3 etc we find that {6, 8, 10} or {9, 12, 15} etc also satisfy $a^2+b^2=c^2$. A more interesting way to generate infinitely many Pythagorean Triples is as follows:
First write down a list of all the square numbers:
1 4 9 16 25 36 49 64 81 100 121 144 169 …
Now look at the differences between successive squares:
3 5 7 9 11 13 15 17 19 21 23 25 …
The second sequence is of course just the odd integers, so among them are infinitely many squares: $3^2=9$, $5^2=25$, $7^2=49$ and so on. Taking each odd square (from the second list) together with the two squares from the first list whose difference is said odd square gives us the following Pythagorean triples:
{3, 4, 5} since 16+9=25
{5, 12, 13} since 144+25=169
{7, 24, 25} since 576+49=625
{9, 40, 41} since 1600+81=1681
And so on. I’ve highlighted the odd squares that give rise to these triples ($3^2=9$, $5^2=25$, $7^2=49$ etc) and also the pairs of squares from the first list whose difference is said odd square. Unfortunately, as the odd squares are getting further apart, it quickly becomes impractical to generate these triples by writing out the two lists (squares and their successive differences) as described above, waiting for an odd square to appear in the second list, so I went about trying to find an algebraic formula to generate the triples.
To my delight, I discovered that the middle numbers of each triple 4, 12, 24, 40, 60, … are not only all multiples of 4, but are none other than 4 x the triangular numbers.
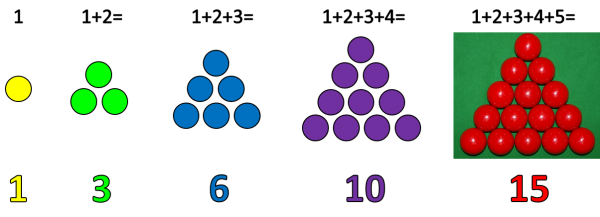
The Triangular Numbers really easy to recall: just picture triangles of snooker balls as above. It’s now easy to generate a Pythagorean Triple of the form {a, b, b+1} (please note there are also infinitely many other Pythagorean Triples!):
In this example, we have generated the triple {13, 84, 85}.
Those who wish to verify the method can check that $(2n+1)^2+(2n^2+2n)^2=(2n^2+2n+1)^2$
In this way we get a pleasing correspondence between two mathematical objects related to triangles: the Triangular Numbers and a certain set of Pythagorean Triples.
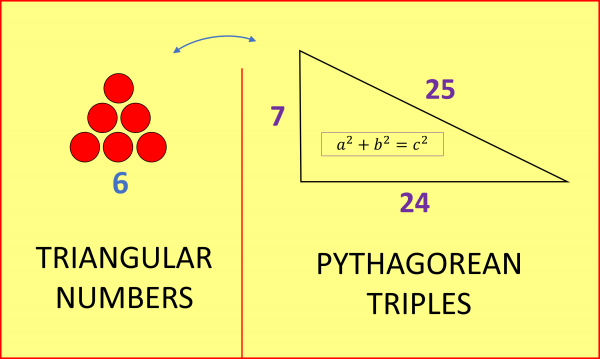
More on Triangular (and Tetrahedral) numbers at How Many Gifts in The Twelve Days Of Christmas.
[mc4wp_form id=”399″]