THREE is the corners (or sides) of a triangle, the somersaults in a triple and the wheels on a tricycle. Three is the notes in a triad, the musicians in a trio, and the tricks in a hattrick. Three is the Musketeers in Dumas’ classic novel. Three is the only number which is both prime (only two factors that go into it) and triangular (1+2). Trigonometry – the huge branch of mathematics dealing with sin, cos and tan, literally means “measuring triangles”.
TWO BABIES PUZZLE: two babies are born to the same mother on the same day of the same year at the same hospital, yet they are not twins. The explanation?: they’re two in a set of triplets.
THIRD TIME LUCKY: A STRANGE SAYING?: If the “early [first?] bird catches the worm” and the “second mouse gets the cheese”, then why do we say “third time lucky”? I’m sure this is said just to make you feel better after having already failed twice!
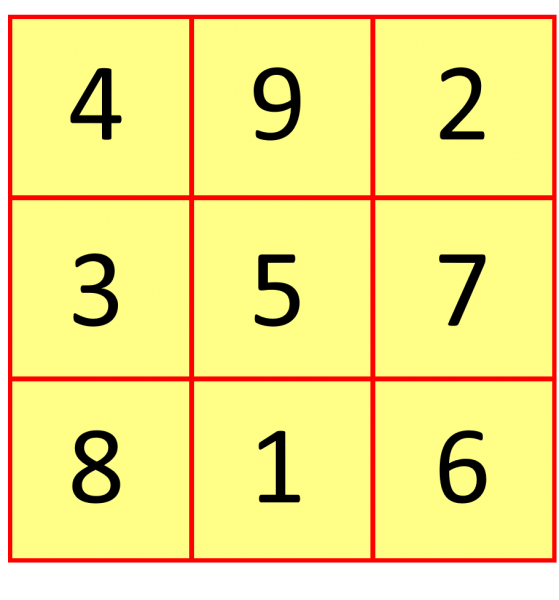
MAGIC SQUARES: A Magic Square is a square array of integers (whole numbers) all of whose rows, columns and diagonals add to the same total. Usually, all the numbers have to be different, in which case there is no 2×2 magic square so the smallest is this 3×3 magic square (or one of its reflections / rotations):
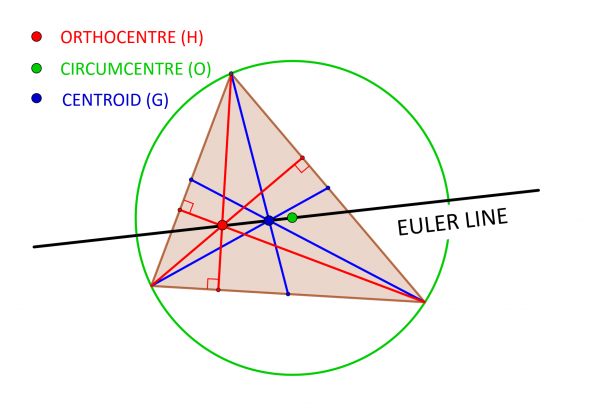
TRIANGLES AND THE EULER LINE: triangles are the simplest possible polygons, having the minimum three sides. Triangles have a number of different points that could reasonably considered to be their “centre”, three of which, incredibly, always lie on the same straight line – the Euler Line. They are the Orthocentre (H: drop a perpendicular from each corner to the opposite side; the Orthocentre is where these three “altitudes” meet – shown in red), the Circumcentre (O: centre of the circle that passes through all three corners, shown in green) and the Centroid (G or “centre of mass”: join each corner to the middle of the opposite side; the Centroid is where these three “medians” meet, shown in blue).
THREE POINTS DEFINE A CIRCLE: Take any three non-collinear (not all lying in the same straight line) points on a page: there is exactly one circle going through all three (if they all lie in a straight line then you cannot draw a circle through them). This marvellous property of the number 3 means that:
TRIPODS: a tripod (or a traditional 3-legged stool) will always stand firmly, even on uneven ground. Anything with four legs (such as a chair) will normally wobble if placed on a wonky slope. Before you go stuffing a folded napkin under the offending leg of a wobbly 4-legged table, here’s an even better solution: TURNING A WOBBLY TABLE WILL ALWAYS FIND A WAY TO MAKE IT STEADY! I’m assuming here that the table has 4 legs of equal length, and that the ground it stands on at least undulates smoothly. Here are the details: https://www.scientificamerican.com/article/strange-but-true-turning/
THREE DIMENSIONS: the world we inhabit has three dimensions: left&right, up&down, forward&backward. Three coordinates are required to specify exactly where we are in space. If you’re a flatlander such as a stick-person drawing or a polygon, then the flat piece of paper you live in is a 2-dimensional world. Here’s how wonderful life in the 4th dimension would be!
More fun facts on this website about the number one, the number two and the number eleven.