
OCTAGON-INTO-QUADRILATERALS

WHAT FRACTION IS SHADED RED?
“Geometry” is a posh word for “shapes”. Here are two fun geometry puzzles for you, inspired by a question form the UK Mathematics Trust Challenge. Anyone can play, even non-mathematicians:
OCTAGONS INTO PENTAGONS: Let’s start with puzzle number one.
It’s fairly easy to find this dissection of the octagon into pentagons, by just slicing it vertically and horizontally rather than across the diagonals:
 OCTAGON-INTO-PENTAGONS
OCTAGON-INTO-PENTAGONS
OCTAGONS INTO HEXAGONS: this is just a little trickier. To begin with imagine the octagon sliced into triangles, rectangles and one central square, like this:

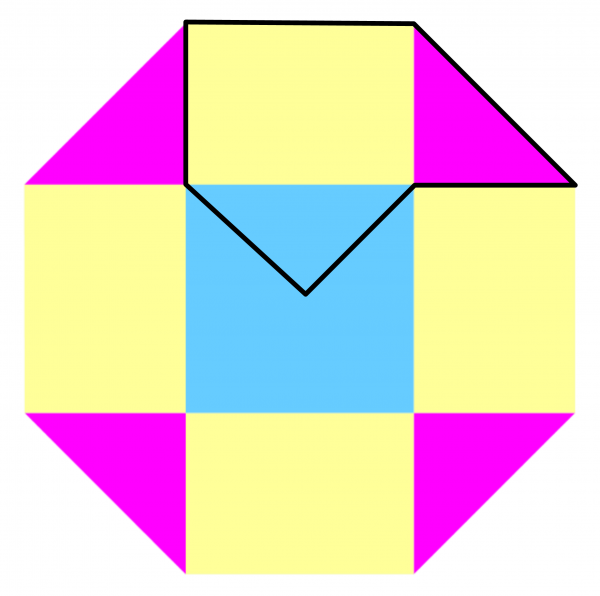
If we can dissect the octagon into four congruent pieces, it seems reasonable that each quarter should consist of one of the triangles, one of the rectangles and a quarter of the central square – like in the second image. And so we have this dissection of the octagon into four congruent hexagons:

OCTAGON-INTO-HEXAGONS
GETTING ZIGGY WTH IT: BEYOND THE HEXAGON: If you’re really on the ball, you might have noticed another way to think of this dissection: it’s the original “octagon-into-quadrilaterals” dissection that we started with, but with each of the four straight-line “spokes” replaced with a zig-zag. If instead you replace each spoke with a zig-zag-zig, you will end up with an octagon dissected into four congruent octagons (8 sides)! Using instead four zig-zag-zig-zags in place of the spokes gives an octagon dissected into four decagons, and so on. In a similar way when n is odd, we can dissect the octagon into four congruent n-sided polygons by replacing the spokes on the “octagon-into-pentagons” dissection with increasingly ziggy zig-zags!
WHAT FRACTION IS SHADED? we now return to the second of the original problems: to determine what fraction of the red-and-white octagon is shaded red. See if you can guess the answer and see if you can prove it, before reading on. I will then present two approaches to answering the puzzle: a slightly involved one to start with that requires some secondary school maths, and then a simple geometrical argument.
THE METRIC APPROACH: let’s assume the short sides of each triangle have unit length. By Pythagoras’ Theorem, the long side has length $\sqrt{2}$ and so do all the sides of the original octagon. The area of each section is shown, and you can check that the red areas sum to $2+2\sqrt{2}$ same as the unshaded area. Incredibly, the answer is that $\frac{1}{2}$ of the octagon is shaded red.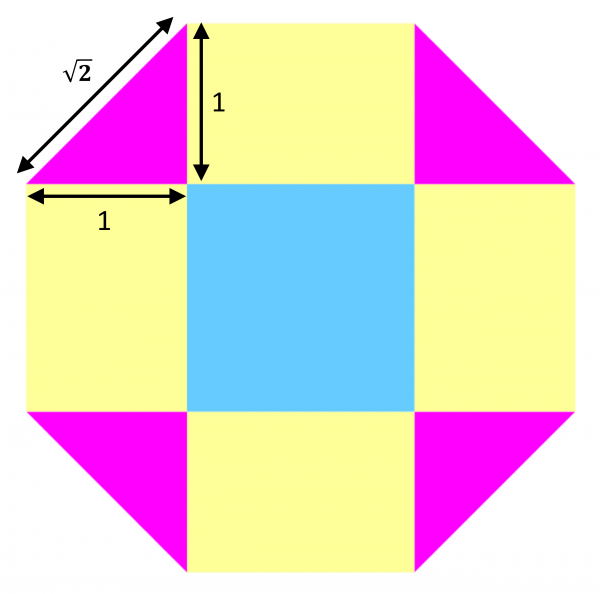
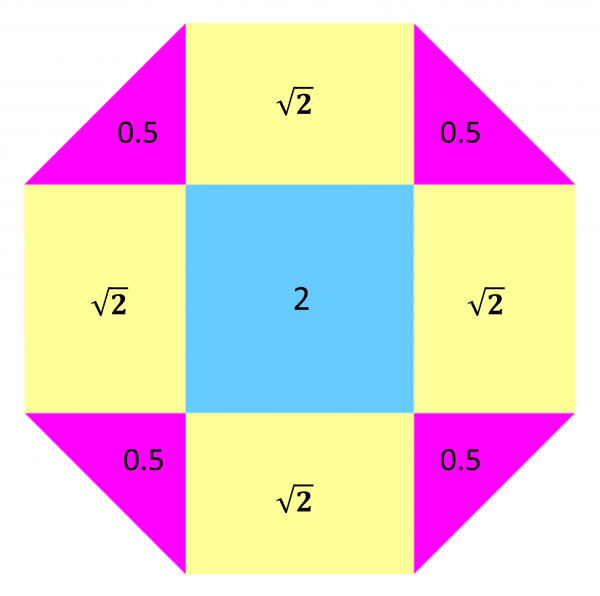

THE SIMPLE GEOMETRICAL APPROACH: look again at the red-and-white image, and again partition it into triangles, rectangles and a central square. The total red area consists of two rectangles and the four triangles, while the white area consists of two rectangles and a square. These two areas are therefore the same if we can rearrange the four pink into triangles to make one blue square. We can do this by simply squishing the four triangles together and rotating through $45^\circ$
A FINAL CONFESSION: this post is both an appreciation of the beauty of the regular octagon, and also an excuse for me to practise my skills at Geogebra – free software for graphing algebraic curves, and drawing pictures of octagons.