House of Maths School Workshops Primary & Secondary in Dorset & South - PARALLAX, PENTAPRISMS AND PHOTOGRAPHY

This is the story of rotations, reflections and enlargements and translations. It’s about an ingenious shape that lives in millions of households yet that few people have even heard of. And it’s the story of how some simple maths – GCSE transformations and a little geometry – led to a revolution in photography. This is the story of the Roof Pentaprism: a simple yet beautiful solid shape at the heart of every DSLR camera (that’s the posh ones!).

WARM-UP: write a word and look at it in a mirror. You’ll see that the word is now backwards: it has been REFLECTED HORIZONTALLY (like a reflection “in the y-axis”). Now place the mirror in different positions: on the floor, near the ceiling, on a wall – and look at your writing through the mirror. What happens to the writing each time? Can you guess what will happen if you look at it through 2 or more mirrors? You should find that a vertical mirror flips the word horizontally and vice versa; with two or more mirrors almost anything is possible!

PARALLAX: Before we meet the Pentaprism, let’s look at a straight forward problem in photography: lining up the shot. To do this, most cameras have a VIEWFINDER, but as this image shows, viewfinders can lead to “parallax” problems. A simple demonstration of parallax is to hold up one finger about an inch in front of your nose; now close each eye in turn and watch as your finger appears to move side to side against the background. Voila: parallax! The same problem occurs with a camera as the viewfinder lies to the side of the camera lens: in this example, a photographer has lined up a shot beautifully through the viewfinder, only to discover that in the actual photo, Fred has a tree coming out of his head. Oh dear!

REFLEX MIRRORS: To get both viewfinder and lens to see the exact same image, we can simply place a mirror at the back of the camera lens at 45°angle to reflect the light away from the camera, and then a second mirror to redirect the light through the viewfinder, like this.

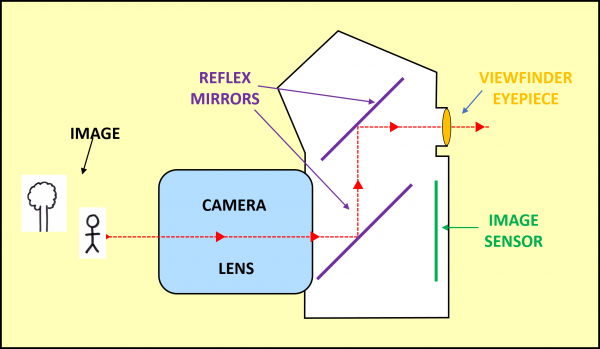
The mirrors are called “reflex” because they reflect (nothing to do with angles larger than 180°). Now the real fun begins, because a focussing camera lens shrinks the image and REFLECTS it upside-down and back-to-front – something we can do in one go at GCSE using an ENLARGEMENT WITH NEGATIVE SCALE-FACTOR:

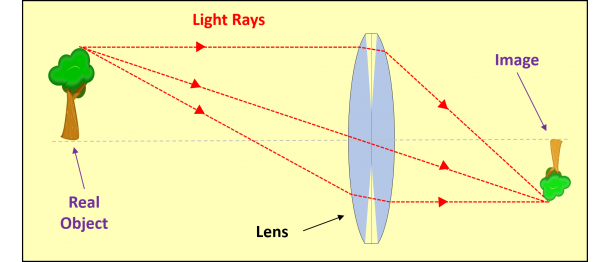
Our two-mirror arrangement does nothing to fix this upside-down-back-to-front-ness: AND THIS IS WHERE THE MATHS SAVES THE DAY in the form of: the PENTAPRISM!!

Let’s replace the upper mirror with a glass prism. Its cross-section is a pentagon with one angle of 90° and the other four angles at 122.5° (since the angle sum in any pentagon is 540°).

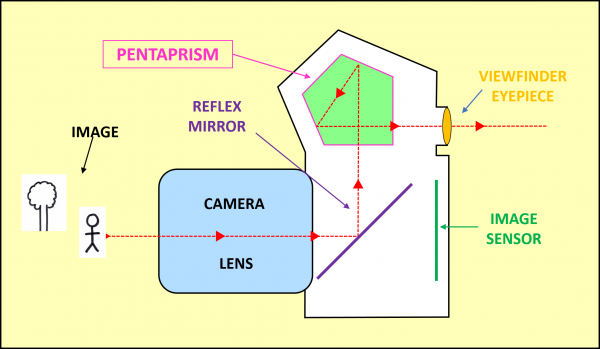
LET’S FOLLOW THE LIGHT RAYS CAREFULLY: the lens REFLECTS the image, leaving it both upside down and back to front; the single mirror then REFLECTS it vertically, it’s now the right way up but is still back-to front; the Pentaprism now ROTATES the light beams through 90° while REFLECTING it vertically twice: these two reflections cancel each other out. We now have an image that just requires one horizontal flip to correct the back-to-front writing (technically called the “handedness” as in right or left handedness). To achieve this, maths came up with a cunning solution: replace one of the pentaprism’s reflecting surfaces with TWO surfaces meeting at 90° – and the ROOF PENTAPRISM was born!

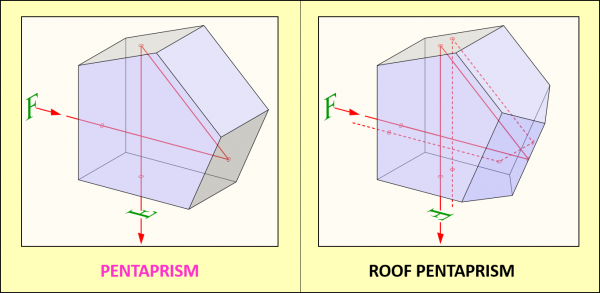
(These two images by DrBob at the English language Wikipedia )

We now have: The Single Lens Reflex (SLR) camera, although most SLR’s are now Digital: hence the DSLR camera, beloved of all pro and serious amateur photographers.

I love the ingenuity with which maths solved the parallax problem for photography, and the way it ties in with so much of the geometry (“shape”) that we learn at school. House Of Maths salutes the mighty Pentaprism!

Comments welcome at House Of Maths Facebook page.

NOTIFY ME OF NEW POSTS BY EMAIL (approx monthly):

[mc4wp_form id=”399″]