NETFLIX: the Producers of instant cult TV series “Stranger Things” clearly appreciate the wonder of the number Eleven: they even (or should that be “oddly”) named the series’ main character “Eleven”.
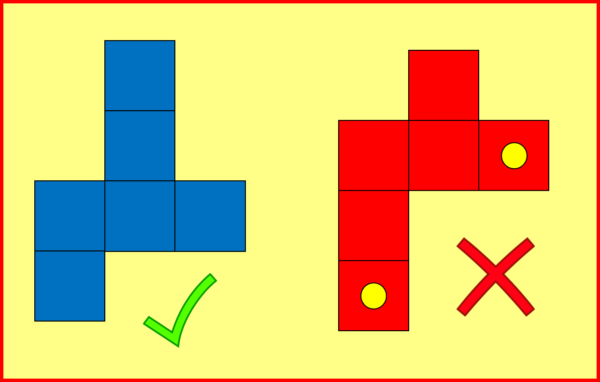
CUBE NETS: there are eleven distinct nets of cubes. A cube net is a (flat) arrangement of six squares that “fold up” to make a cube. An example is the hexomino (six joined squares) on the left, but not the one on the right (in which the two marked squares fight to become the same face of the cube).
OCTAHEDRON NETS: rather wonderfully, there are also exactly eleven distinct nets of the octahedron! If you’ve not met one yet, the Octahedron is a regular 3D shape with 8 triangular faces (think of it as two square-based pyramids with their square faces glued together). The cube and octahedron are “dual polyhedra“: the cube has 6 faces and 8 vertices (like 3D “corners”) whereas the octahedron has 8 faces and 6 vertices. They both have 12 edges. If you take a cube (or octahedron), replace each face with a vertex and each vertex with a face, then join the new vertices together, you get an octahedron (or cube). Magic! It’s this “dual” property that means both shapes have the same number of nets: eleven. For the same reason, the regular Dodecahedron and Icosahedron also have the same number of distinct nets: 43380.
DIVISIBILITY TEST: it’s easy to see if a (whole) number is divisible by ten: just see if it ends in a zero. And a multiple of five will always end in 0 or 5. The test for divisibility by 3 is slightly more cunning: you take the digit sum e.g. 1062 is divisible by 3 because 1+0+6+2=9, which is divisible by 3, and therefore so is the original 1062.
Rather fabulously, the test for divisibility by eleven is to look at the alternating digit sum: just alternately add and subtract consecutive digits, if the result is divisible by 11 then so is the original number e.g. try 92818. We see that 9-2+8-1+8=22, which is divisible by 11, therefore so is 92818 (it’s 11×8438).
ALL PALINDROMES WITH AN EVEN NUMBER OF DIGITS ARE DIVISIBLE BY 11: e.g. 7337=11×667, or 623326=11×56666. Can you see why this is true? (HINT: use the “alternating digit sum” divisibility test).
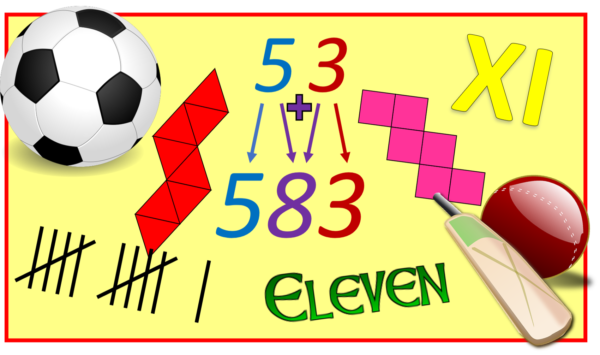
SPORTS TEAMS: there are 11 footballers on each side, and 11 cricketers in a team. Could this perhaps be because 11 is a prime number? A team of, say, ten members might naturally split into two groups of five, harming the team dynamics?
TIMES TABLE: finally, of course, eleven is everyone’s favourite times table. To multiply a one-digit number by eleven, merely repeat that digit e.g. 11×5=55. To multiply a 2-digit number by 11 is only marginally harder: pull the two digits apart and put their sum in the middle e.g. 11×53=583 (since 5+3=8).
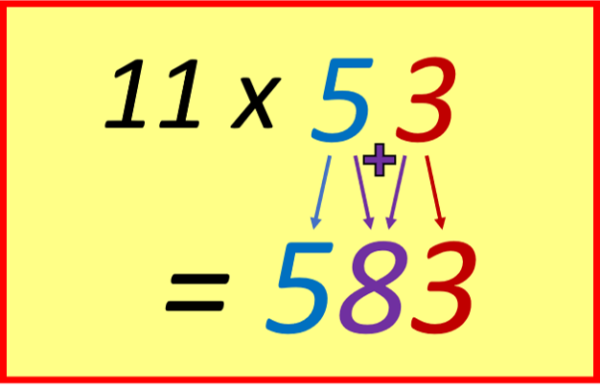
This sometimes involves a “carry” e.g. 11×68=748 because 6+8=14 so in the hundreds column the 6 becomes 7.
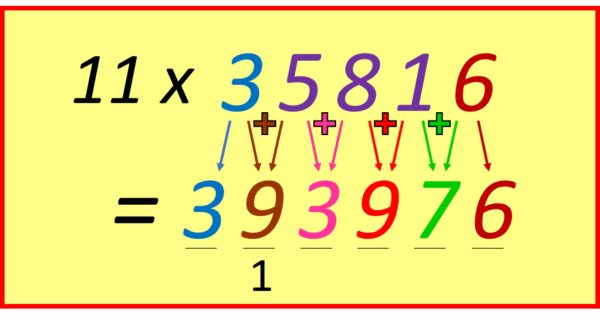
MULTIPLYING A LONGER NUMBER BY ELEVEN: this is a “magic trick” that never fails to impress! Simply start at the units end, and add successive digits, placing the sum in between, like this:
NOTIFY ME OF NEW POSTS BY EMAIL (approx one a month):
[mc4wp_form id=”399″]