This is Giants Causeway on the North Coast of Northern Ireland, famed around the world for its awe-inspiring hexagonal stone plinths. Incredibly, the stones are built not by a genius mathematician or engineer but by mother nature. In this article I’ll explain how it is that nature can afford us such a beautiful display.

The plinths here are in fact igneous basalt columns, created when molten lava comes up from inside the earth and cools. As the rock cools it contracts, and this changing shape means that as it solidifies the rock must crack to release the pressure (similar to the way that an ice cube warms, contracts and cracks when you put it into your drink).
The question is: what shape should the surface of the lava crack into? Let’s make life easy for mother nature and give her a choice of the regular shapes proven by mathematics to be the only three that tesselate (completely cover a flat area without leaving any gaps): the triangle, square and hexagon. (Yes it’s true that nature could choose something more complicated such as the beautiful 3464 tesselation and use a combination of all three, or even the 4-6-12 tesselation that uses dodecagons too, but nature is incredibly efficient and tends to choose the easiest solution to a given problem!).
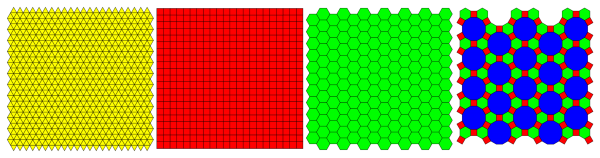
TESSELATIONS: TRIANGLES, SQUARES, HEXAGONS; 4-6-12 (SEMI-REGULAR)
Of those three, nature being efficient and beautiful will choose the solution that minimises the amount of cracking it has to effect. So let’s suppose there must be a crack every square foot of area, so that any given point is reasonably close to a crack. (any mathematician who dislikes Imperial units may click here to read about the system’s benefits – which include being convenient for approximate measurements). You can check that a triangle with an area of 1 must have a perimeter of $\sqrt[4]{432}\approx{4.56}$, a square can enclose 1 square foot with a smaller perimeter of 4, but the winner is the hexagon, which can enclose a unit area with a perimeter of just $\sqrt[4]{192}\approx{3.72}$. You may prefer to argue that of course the hexagons have the smallest perimeter of the three, as they are closest in shape to the circle (which encloses a given area using the least perimeter).

THE WINNER IS… THE HEXAGON!! Had the lava at Giants Causeway been spewed forth evenly and cooled uniformly, the whole area would be covered in perfect hexagons. Because things are rarely so perfect in the real world, I did during my visit find some rogue pentagons, heptagons and even octagons sprinkled amongst the hexagons. You can also find hexagonal basalt columns in Scotland, California, Israel, Japan, Iceland, Mexico, Russia, Vietnam and many other locations worldwide. But the hexagons of Giants Causeway are perhaps the most famous, and are well worth a visit for anybody but especially for mathematicians!
