Circles are very special – more so than rectangles. Rectangles, you see, come in many different sizes (big, small, enormous etc) and also in many different shapes (tall and thin, short and stubby, square etc).
Circles also come in many different sizes (big, small, enormous etc.) but unlike rectangles, all circles are exactly the same shape. That’s right: even if two circles have different circumference (the distance all the way around the outside) and different diameter (the distance across the middle from one side to the other) the two will always be in the same ratio. This ratio of C/D (circumference divided by diameter) always gives the number $\pi$ (pronounced “pi” – but nothing to do with the pie that you eat with chips, peas and gravy).
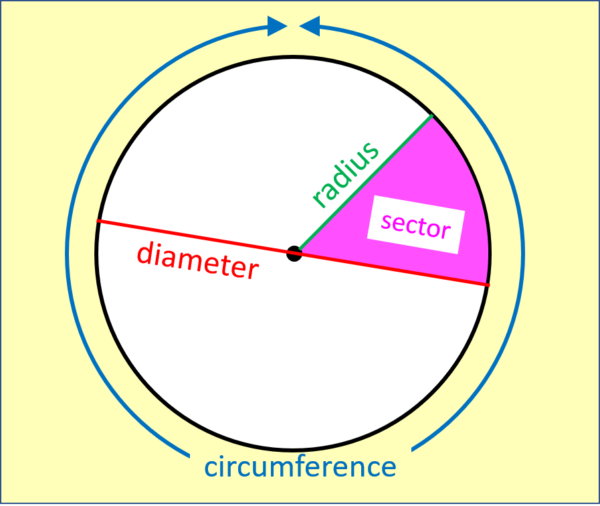
Yes! Find any circle – maybe a plate, the end of a thick candle, or the circle at the top of the kitchen bin. Measure the circumference and the diameter, and you will find the circumference is always 3 and a bit times (actually $\pi$ times) as long as the diameter.
It turns out that if you write $\pi$ as a decimal, it goes on forever. Here are the first 101 digits of $\pi$. Nobody can spot a pattern in this jumble, so if you can then get ready to become rich and famous! Some people like to see how many digits they can commit to memory; if you’re one of them then this mnemonic will help you get started: How I Wish I Could Recollect Pi Easily Today: counting the letters of each word gives you the first few digits.
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 …
But even that’s not exact because decimal pi goes on forever! In fact, if you search through enough digits of $\pi$ you will definitely find your birthday hidden in there somewhere (mine starts at position 8533). You can’t write $\pi$ out exactly in decimal form unless you have an infinitely big piece of paper and unlimited amounts of ink (even then you would probably get writer’s cramp after the first gazillion digits).
How about a fraction? Amazingly, you can’t write it as a fraction either! $\pi$ is roughly $3\frac{1}{7}$, but that’s not exact, it’s just a fairly good approximation. To get round the problem of how to write it, mathematicians used to refer to this “three and a bit” by saying:
quantitas in quam cum multiflicetur diameter, proveniet circumferencia
Ooh, snappy! Eventually, someone really clever (Welshman William Jones) came up with the symbol $\pi$. Celebrity maths boffin Euler soon started using it too, and now everyone uses the symbol $\pi$.
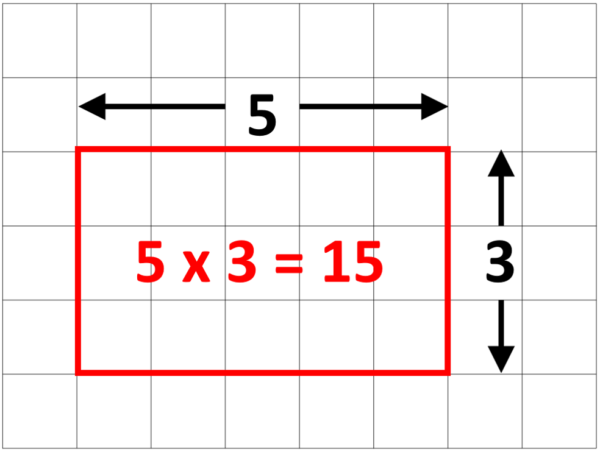
The whole point of numbers is that they allow us to measure things (how many? how big? how hot? how strong? how many likes? etc etc the list goes on forever, just like the digits of $\pi$). One thing mathematicians love to measure is area because it tells us how much space objects take up on the page. It’s easy to see that the area of a rectangle is given by multiplying together the length and the width: if you don’t believe me just count the squares on the inside of this rectangle:
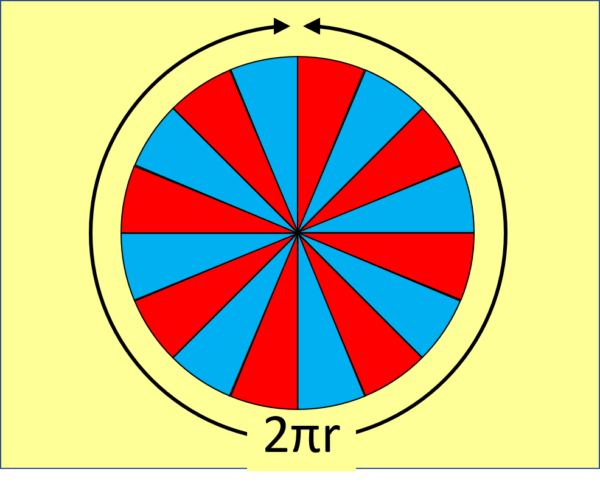
To see how big a circle is, we can cut it up into lots of thin slices (called sectors) like this:
and then rearrange the sectors to make a shape that looks very much like a rectangle, like this:
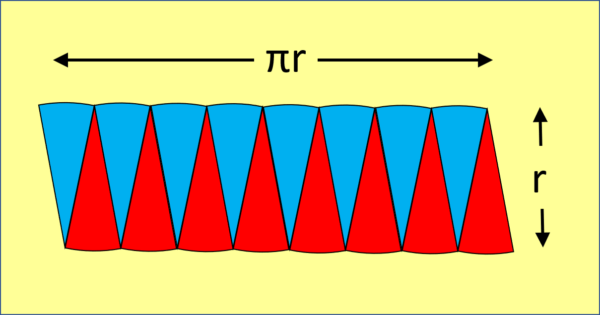
Doing this doesn’t change the area because we’re just rearranging the pieces, we’re not making them bigger or smaller. The height of this “rectangle” is just r – the radius of the circle. The length of the “rectangle” is made up of 8 short arcs, and their total length is just the distance around the original circle, or half the circumference, so half of $\pi$ x diameter, which is just $\pi$ x radius (because radius is by definition half of the diameter). So the area of the circle = area of the “rectangle” = length x width = $\pi$ x r x r = $\pi$r2. It’s not exact yet, BUT we can make it as exact as we like by slicing the circle more and more thinly into thinner and thinner sectors which, when rearranged, will get closer and closer to an exact rectangle shape. So “in the limit” (a posh term mathematicians use to explain why we can pretend it’s exact) as the sectors become thinner and thinner, the area of a circle is exactly $\pi$r2.
Instead of reading this blog, you could have read these two short algebraic formulae instead:
(Algebra, you see, is a great way to say a lot of maths with hardly any writing).
NOTIFY ME OF NEW POSTS BY EMAIL (approx one a month):
[mc4wp_form id=”399″]