I’m super proud of this workshop because the children really love doing the maths (they always want to carry on when the session is over) and I’m not aware of anyone else who is doing it. The challenge is to put each set of tiles together so that the white circle is completely covered – no gaps!
AT SIX: REGULAR POLYGONS!
Triangles, squares and hexagons all tesselate (they fit together to tile as large an area as you like without leaving any gaps). Can you satisfy yourself that regular pentagons do not? HINT: put three together, how will you now fill the remaining gap? The tesselations made from regular triangles, squares and hexagons are sometimes known as deltille, quadrille and hextille. With 3 colours, you can do each of these so that tiles which touch are different colours. This is a really popular starter for my hands-on Maths Workshop for Year 2.



AT FIVE: IRREGULAR TRIANGLES AND QUADRILATERALS!
Rather wonderfully, all triangles and quadrilaterals can tesselate the plane even if they are not regular! (The same is not the case for hexagons). To create a tesselation from any triangle: rotate it $180^{\circ}$ about the midpoint of any side and join to the original to make a parallelogram, then it’s easy to tesselate the parallelograms. To create a tesselation from any quadrilateral: rotate the quadrilateral through $180^{\circ}$ about the midpoint of each of its sides, then use translations. This works because the four interior angles of any quadrilateral and also the angles around a point both add up to $360^{\circ}$. In the rotation construction above, each corner of the quadrilateral will make one appearance at each vertex of the tesselation. BEWARE: The pictured tesselation won’t work if some of the tiles are flipped over!

AT FOUR: ARCHIMEDEAN TESSELATIONS!
You cannot tesselate using just regular octagons BUT it is possible to tile the plane using a combination of octagons and squares. We can call this a 4-8-8 tesselation, because moving clockwise around each vertex (where three or more tiles meet) we can see a square (“4”) then two octagons (“8”, “8”). The other seven Archimedean Tesselations (patterns that tile the pane using more than one type of regular polygon) are: 3-4-6-4; 3-6-3-6; 3-12-12; 4-6-12; 3-3-3-3-6; 3-3-3-4-4; 3-3-4-3-4. The last two are two different ways of tesselating the plane using just triangles and squares: in 3-3-3-4-4 each squares touches two others along an entire edge, but in 3-3-4-3-4 two squares only ever meet at at point. Here is a 3-3-4-3-4 tesselation from my Maths Club Tesselation Workshop (this one is pretty tricky- I don’t give it to Year 2 !!).

AT THREE: POLYOMINOES and POLYIAMONDS!
These are so cool: a polyomino is a shape made by gluing squares together along their edges. One square is called a monomino, two glued together make a domino, three make a triomino (there are two different ways to do this), then come tetrominoes, pentominoes, hexominoes and so on. My hands-on-maths-workshop for schools includes your chance to tesselate both the H hexomino (pictured) and the T tetromino. Year 2 probably enjoy the H most out of all my tiles!

Rather wonderfully: all polyominoes up to size six tesselate! (So all hexominoes, pentominoes, tetrominoes, triominoes and of course the domino and monomino or ‘square’). There are however two heptominoes (7 squares glued together edge-to-edge) that stubbornly refuse to tesselate: how annoying! CHALLENGE: can you join 7 squares to make a heptomino that does not tesselate?
Similar to polyominoes are the POLYIAMONDS – made this time of many equilateral triangles glued together edge-to-edge. The sequence goes: moniamond, diamond, triamond (note that 3 equilateral triangles always join to make an isosceles trapezium), tetriamond, pentiamond, hexiamond etc. Here are some examples (from my Year 2 hands-on workshop) of a tesselating “bat” hexiamond. See if you can picture each “bat” as both a tridiamond (three diamonds joined together) and also a ditriamond (two triamonds joined together!).

AT TWO: SPHINX HEXIAMOND!
You can easily tesselate this particular hexiamond (=6 equilateral triangles joined together) by turning pairs of them (one tile right way up, one rotated upside down) into parallelograms. But a much more fun way is to combine four of them like this to make a larger copy of the original shape:
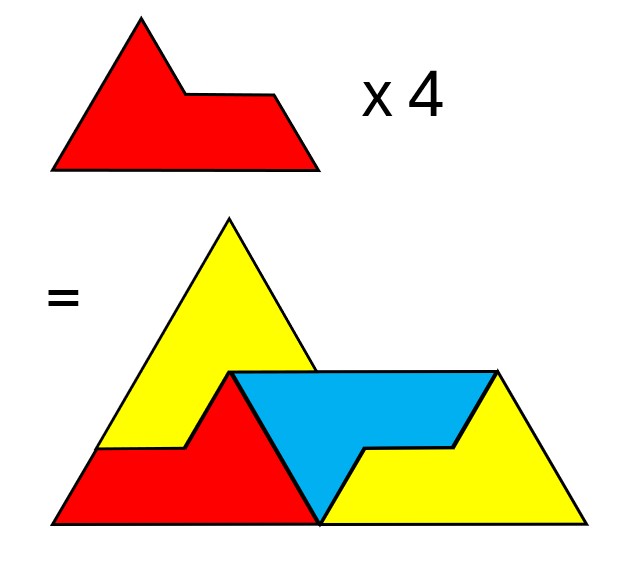
Now you can combine four of these to make an even larger one and so one forever. How cool is that?!! The ability to make larger copies of itself makes the Sphinx Hexiamond an example of a rep-tile. In this context, rep-tiles means “replicating tiles” – not green lizardy things.
AT ONE: OTHER POLYFORMS!
Polyominoes and polyiamonds are both examples of polyforms: a shape made by joining multiple copies of any polygon (a “many-sided flat shape) edge-to-edge. Other fabulous examples (and the basic units they are made from) are polyhexes (regular hexagons joined together) and polykites (kites). I’ve not cut any polyhexes yet but they look really fun. In 2023, English mathematician David Smith announced his sensational discovery of the Hat Monotile – which is a polykite! David’s new tile can tesselate the entire plane, but only in a way that never repeats – how is that even possible?!! I have a set of hat tiles – they are really really tough to fit together because there is no pattern! David was just playing around with fun patterns like you and I are doing right now, but his discovery made him world famous! I wonder how many other people had discovered the hat shape but without realising its special aperiodic property.
BONUS SHAPE: the KRINKLE!
Just after I wrote this blog, expert tesselator Miki Imura announced her discovery of the Krinkle – a whole family of new tiles that tesselate in this new spiral pattern. They are so cool I had to get some cut! Can you spot the pattern? It’s hard, isn’t it – but very fun!!

IS THIS MATHS?
YES – definitely! Maths is not really about numbers: it’s about patterns. They can be patterns in numbers (think of your favourite 9 times table trick), in algebra (which is the language you use to write down patterns), or in shapes (also called geometry). A tesselation is an arrangement of shapes that fit together without leaving any spaces, usually with a pattern too, so this is definitely maths!